In distributed systems, we distribute data on multiple partitions for scalability and performance. For e.g. DynamoDB database spreads data across multiple partitions.

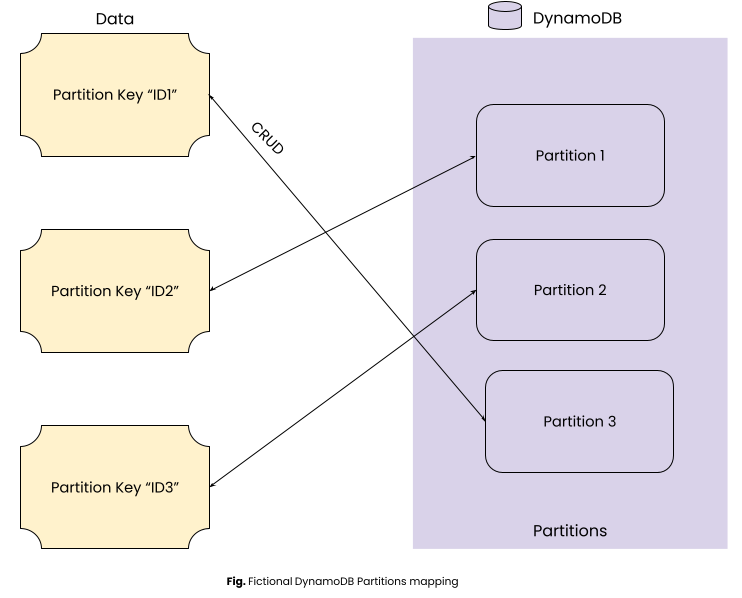
We can see above that a Partition Key impacts which Partition will handle this data.

How does DynamoDB choose the partition based on the Partition Key?

DynamoDB, Cassandra and others use a mapping strategy called Consistent Hashing.

Before understanding a consistent hashing strategy let’s talk about a simpler hashing strategy called Modulo Hashing.

Modulo Hashing

The Modulo Hashing technique finds the target partition by using the following formula:

Partition Index = HashingFunction(Partition Key) % Number of Partitions

The Partition Index starts from 0.

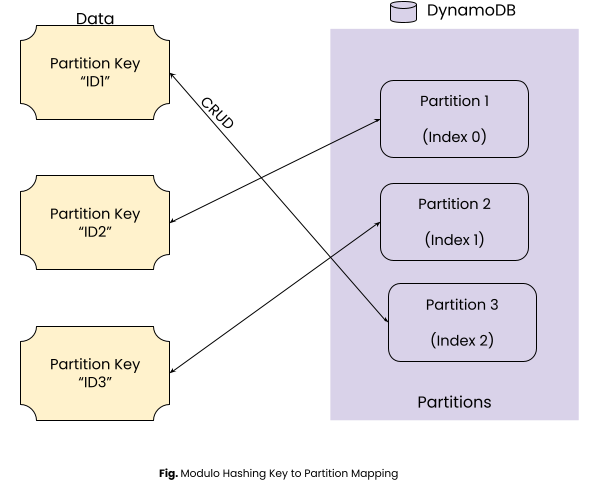
Number of Partitions = 3

hashFunction(“ID1”) = 302; Partition Index = 302 % 3 = 2

hashFunction(“ID2”) = 300; Partition Index = 300 % 3 = 0

hashFunction(“ID3”) = 301; Partition Index = 301 % 3 = 1

Benefit of Modulo Hashing is its simplicity.

Let’s assume we want to add 4 new partitions and it will end up changing the Partition Index for many Partition Keys as the Number of Partitions increases to 7 even if the hash function results in the same value.

Number of Partitions = 7

hashFunction(“ID1”) = 302; Partition Index = 302 % 7 = 1

hashFunction(“ID2”) = 300; Partition Index = 300 % 7 = 6

hashFunction(“ID3”) = 301; Partition Index = 301 % 7 = 0

This strategy if used by DynamoDB will force data movement from one partition to another with every resharding. Similarly if used by a distributed cache will lead to an increased amount of cache miss.

The biggest drawbacks of modulo hashing are:

1. Changes in the number of partitions end up changing partition mapping for a large number of partition keys.
2. Change in partition mapping leads to data movement or other reciprocation like cache hit for distributed cache etc.
3. It makes horizontal scaling complex and inefficient when we dynamically scale up or down very frequently.

Hence this strategy is typically not used apart from testing.

Consistent hashing will help overcome these drawbacks and

Consistent Hashing

In consistent hashing, along with Partition Key, we also hash the partition identifier (server name, IP address etc) with the same hash function. The hash value of the partition key and partition server are within the same hash space. Hash space has a fixed start and end number.

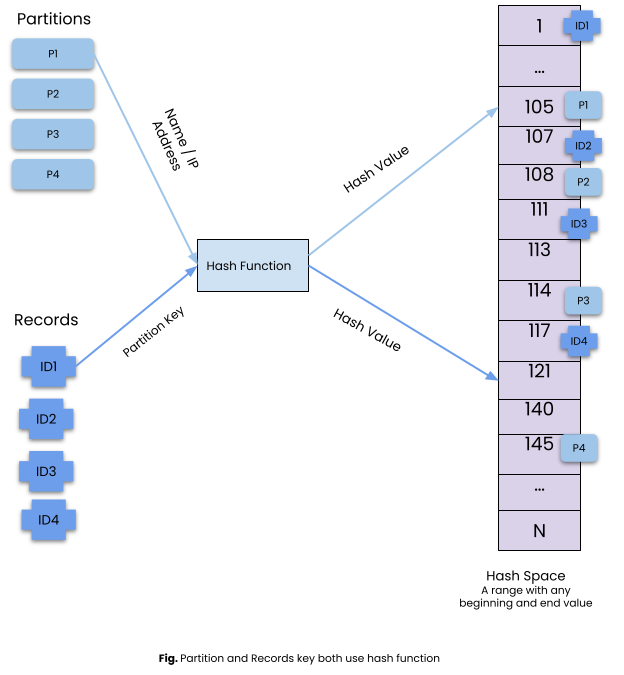
We further take the start and end points on hash space and connect them on a circle.

Let’s say we have four partition servers and several records mapped on the circle based on their hash value.

To map a partition server for a record, we scan for the first partition server on the circle from the record position in the clockwise direction.

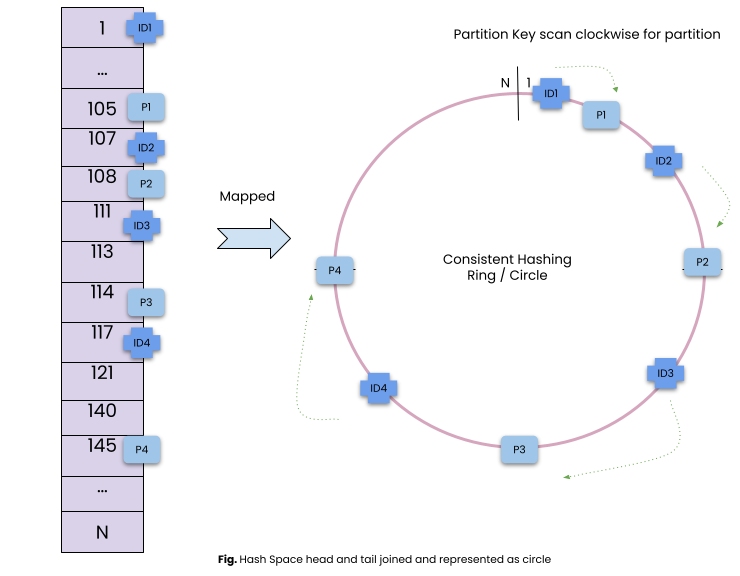
In case we add or remove a partition server, remapping only impacts a few of the partition keys.

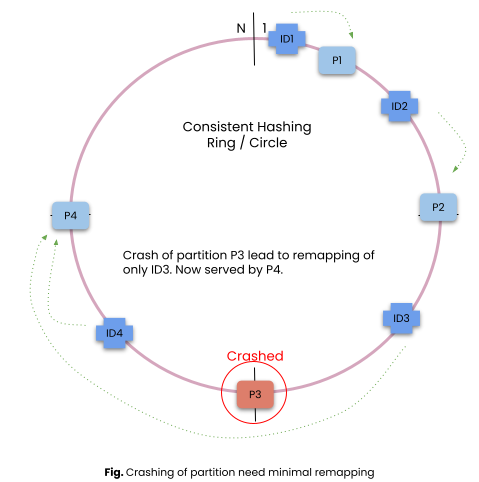
Benefit:

1. In case of addition or removal of partition server, very little partition remapping is required resulting in less data movement or cache misses.

Challenges in Consistent Hashing

Mapping of Partition Server on the circle is typically not even and one server might get overloaded with more partition keys than others.

If the partition server comes and goes frequently the chance of increased load on other partitions increases manyfold.

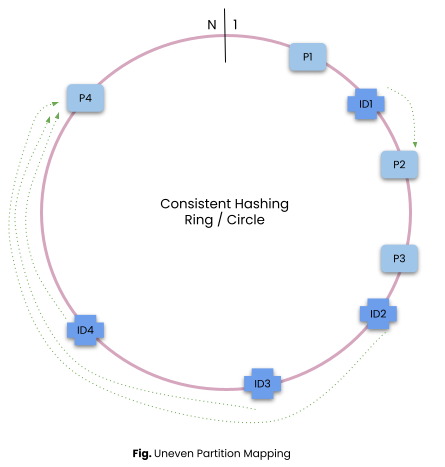
To solve this problem the concept of virtual nodes is used. Two or many virtual nodes are representing the same partition but they appear in different places on the circle.

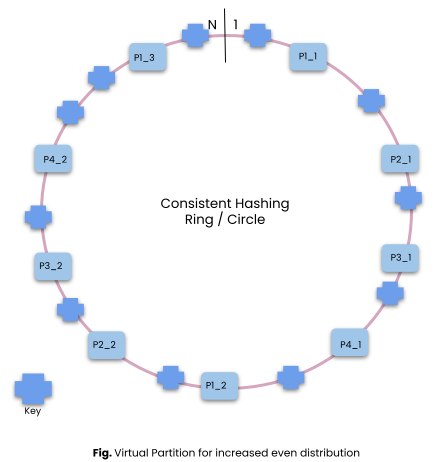
As the number of virtual nodes increases, data gets more evenly distributed.

One downside of the increasing number of virtual nodes is the increased size of the virtual node metadata. This is a tradeoff which we need to keep in mind.

Summary

We described Modulus and Consistent hashing strategies which are often used in data partitioning and load balancing for predictable Key to Server mapping. We talked about the benefits and drawbacks of these strategies.

For further reading on it, a consistent hashing Wikipedia article is good. It also provides a list of products which are using it.

Rendezvous hashing is a better and generally recommended algorithm nowadays.